mosum.py: user guide¶
Installation¶
(.venv) $ pip install mosum
Generating data¶
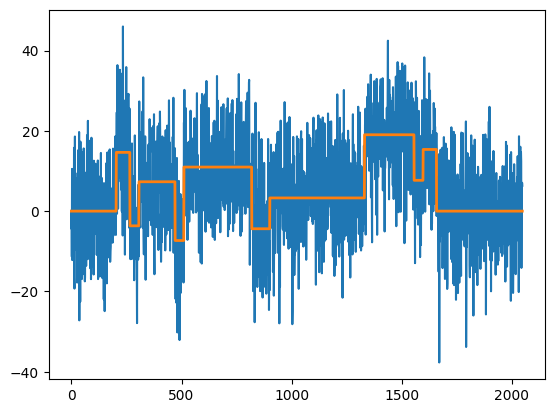
We can simulate data from a mean-change model with testdata. The simulated data is stored in x, and the signal in mu.
[4]:
import mosum
sim = mosum.testData("blocks")
x = sim["x"]
from matplotlib import pyplot as plt
import pandas as pd
pd.Series(x).plot()
plt.plot(sim["mu"], '-', lw=2)
plt.show()
MOSUM procedure¶
The function mosum uses a single bandwidth to detect changes. This returns an object with plot, print, and summary methods.
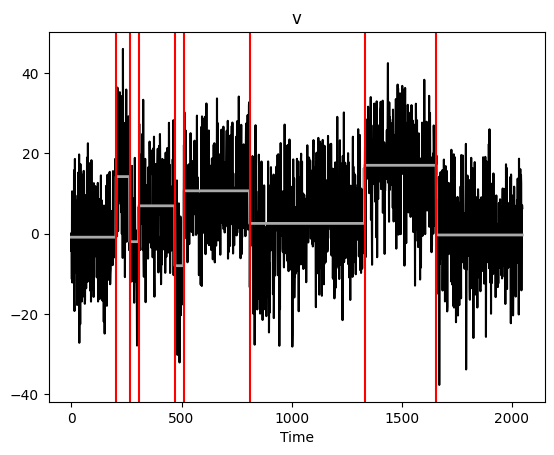
[5]:
ms = mosum.mosum(x, G = 20)
ms.plot()
plt.show()
[10]:
ms.plot(display="mosum")
plt.show()
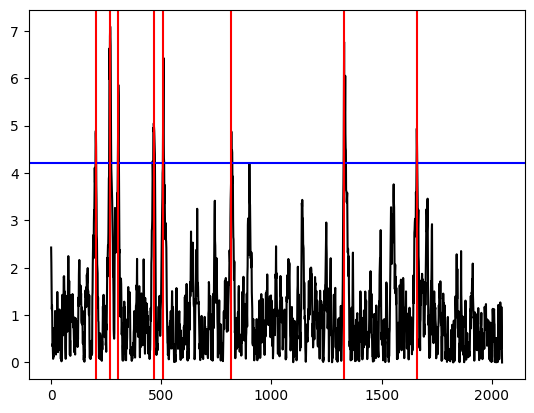
[11]:
ms.print()
change points detected with bandwidths (20,20) at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 203 20 20 0.013 1.547
1 268 20 20 0.000 2.243
2 305 20 20 0.001 1.853
3 466 20 20 0.008 1.597
4 510 20 20 0.000 2.033
5 818 20 20 0.014 1.542
6 1330 20 20 0.000 2.140
7 1660 20 20 0.011 1.562
[12]:
ms.summary()
change points detected at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 203 20 20 0.013 1.547
1 268 20 20 0.000 2.243
2 305 20 20 0.001 1.853
3 466 20 20 0.008 1.597
4 510 20 20 0.000 2.033
5 818 20 20 0.014 1.542
6 1330 20 20 0.000 2.140
7 1660 20 20 0.011 1.562
Multiscale MOSUM procedure with bottom-up merging¶
The function multiscale_bottomUp runs the MOSUM procedure with multiple bandwidths, merging these from smallest to largest. Again, this returns an object with plot, print, and summary methods.
[13]:
%%capture --no-display
ms_multi = mosum.multiscale_bottomUp(x, G = [10,20,40])
ms_multi.plot()
plt.show()
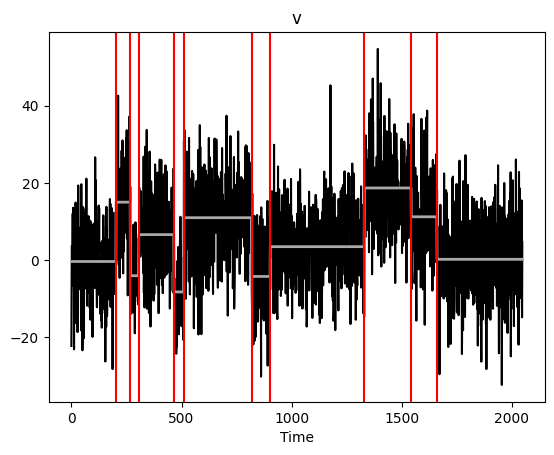
[14]:
ms_multi.print()
change points detected with bandwidths ([10, 20, 40],[10, 20, 40]) at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 268.0 10.0 10.0 0.005 2.365
1 306.0 10.0 10.0 0.039 2.087
2 466.0 10.0 10.0 0.007 2.331
3 818.0 10.0 10.0 0.051 2.051
4 1330.0 10.0 10.0 0.001 2.551
5 203.0 20.0 20.0 0.013 1.547
6 510.0 20.0 20.0 0.000 2.033
7 1660.0 20.0 20.0 0.011 1.562
8 903.0 40.0 40.0 0.015 1.059
9 1543.0 40.0 40.0 0.006 1.130
[15]:
ms_multi.summary()
change points detected at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 268.0 10.0 10.0 0.005 2.365
1 306.0 10.0 10.0 0.039 2.087
2 466.0 10.0 10.0 0.007 2.331
3 818.0 10.0 10.0 0.051 2.051
4 1330.0 10.0 10.0 0.001 2.551
5 203.0 20.0 20.0 0.013 1.547
6 510.0 20.0 20.0 0.000 2.033
7 1660.0 20.0 20.0 0.011 1.562
8 903.0 40.0 40.0 0.015 1.059
9 1543.0 40.0 40.0 0.006 1.130
Multiscale MOSUM procedure with local pruning¶
The function multiscale_localPrune runs the MOSUM procedure with local pruning, removing change point candidates locally to optimise an information criterion. Again, this returns an object with plot, print, and summary methods.
[6]:
%%capture --no-display
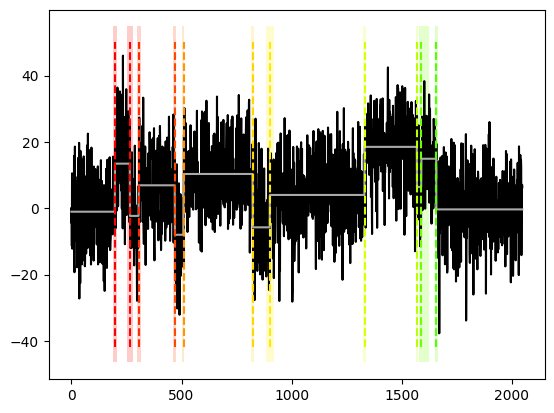
ms_multi_lp = mosum.multiscale_localPrune(x, G = [10,20,40])
ms_multi_lp.plot()
plt.show()
[7]:
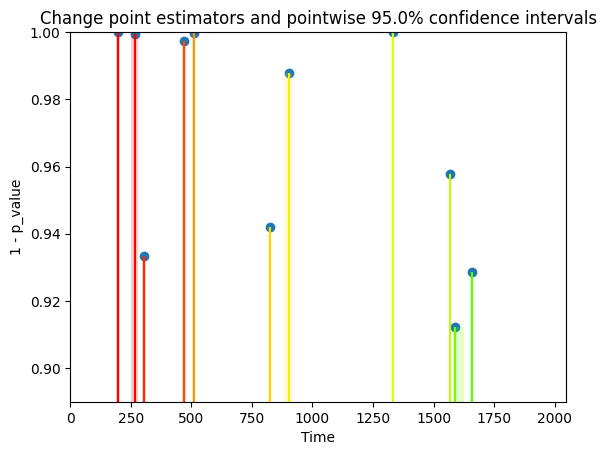
ms_multi_lp.plot(display = "significance")
plt.show()
[18]:
ms_multi_lp.print()
change points detected with bandwidths ([10, 20, 40],[10, 20, 40]) at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 203 10 20 0.056 1.733
1 268 10 10 0.005 2.365
2 306 10 10 0.039 2.087
3 466 10 10 0.007 2.331
4 510 10 20 0.001 2.267
5 818 10 10 0.051 2.051
6 903 40 10 0.062 1.561
7 1330 10 10 0.001 2.551
8 1555 40 20 0.024 1.261
9 1660 20 10 0.025 1.832
[19]:
ms_multi_lp.summary()
change points detected at alpha = 0.1 according to eta-criterion with eta = 0.4 and mosum variance estimate:
cpts G_left G_right p_value jump
0 203 10 20 0.056 1.733
1 268 10 10 0.005 2.365
2 306 10 10 0.039 2.087
3 466 10 10 0.007 2.331
4 510 10 20 0.001 2.267
5 818 10 10 0.051 2.051
6 903 40 10 0.062 1.561
7 1330 10 10 0.001 2.551
8 1555 40 20 0.024 1.261
9 1660 20 10 0.025 1.832
Confidence intervals¶
To obtain confidence intervals, we can specify do.confint = True as an argument to the mosum, multiscale_bottomUp or multiscale_localPrune functions, or use the confint method for the resulting objects.
[25]:
%%script echo
b1 = ms.confint()
b2 = ms_multi.confint()
b3 = ms_multi_lp.confint()
3D visualisation¶
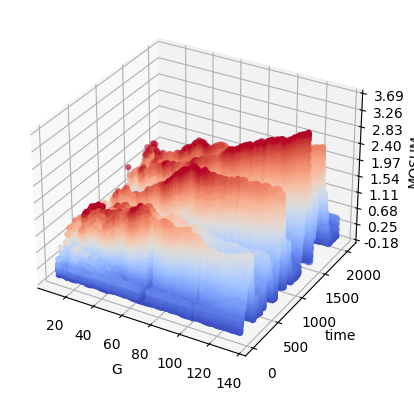
We can visualise in 3D the MOSUM detector at a range of scales, with the heights and colours of the detector corresponding to the size.
[29]:
mosum.persp3D_multiscaleMosum(x)
References¶
Eichinger, B., & Kirch, C. (2018). A MOSUM procedure for the estimation of multiple random change points. Bernoulli, 24(1), 526-564.
Messer, M., Albert, S., & Schneider, G. (2018). The multiple filter test for change point detection in time series. Metrika, 81, 589-607.
Meier, A., Kirch, C., & Cho, H. (2021). mosum: A package for moving sums in change-point analysis. Journal of Statistical Software, 97, 1-42.
Cho, H., & Kirch, C. (2022). Two-stage data segmentation permitting multiscale change points, heavy tails and dependence. Annals of the Institute of Statistical Mathematics, 1-32.
Cho, H., & Kirch, C. (2022). Bootstrap confidence intervals for multiple change points based on moving sum procedures. Computational Statistics & Data Analysis, 175, 107552.